Výskum v oblasti dynamických modelov správy finančných a iných portfólií je predovšetkým orientovaný na dynamické stochastické programovanie s cieľom maximalizácie cieľového úžitku vzhľadom na dynamicky meniace sa váhy jednotlivých súčastí portfólia. Využívame nástroje založené na riešení Hamiltonovej-Jacobiovej-Bellmanovej parciálnej diferenciálnej rovnice a jej vhodnej transformácii. Navrhujeme efektívne a stabilné numerické schémy riešenia príslušných rovníc. Výsledky aplikujeme predovšetkým v oblasti dynamického optimálneho riadenia dôchodkových penzijných fondov.

Výskum je zameraný na teoretické a výpočtové štúdium dynamiky komplexných kvapalín a jej aplikácie do iných oblastí ako je mechanické a chemické inžinierstvo, náuka o materiáloch a geofyzika. Matematické aspekty výskumu zahŕňajú teóriu asymptotického škálovania a redukcie riadiacich diferenciálnych rovníc, teóriu stability a bifurkácií, poruchové a asymptotické metódy, a numerické metódy pre parciálne diferenciálne rovnice.

Obálková analýza dát (Data envelopment analysis, DEA) je neparametrická metóda v operačnom výskume na meranie relatívnej účinnosti rozhodovacích jednotiek na základe techník matematického programovania. V našom výskume sa zameriavame na aplikáciu teórie a metód konvexnej optimalizácie s cieľom poskytnúť jednotnú analýzu DEA modelov, na štúdium environmentálnych DEA modelov a na navrhovanie výpočtových metód pre vysokorozmerné DEA modely. Pracujeme tiež na implementácii programových kódov pre širokú škálu lineárnych a nelineárnych DEA modelov a súvisiacich problémov.
Výskum v oblasti skúmania dynamiky vývoja krivosťou riadených tokov kriviek a plôch je zameraný na kvalitatívne a numerické aspekty. Zameriavame sa aj na štúdium nelokálnych geometrických tokov zachovávajúcich geometrické veličiny, akými sú plocha alebo dĺžka. Zvláštna pozornosť je venovaná návrhu numerických schém, ktoré sú optimálne z pohľadu rozmiestnenia diskretizačných bodov na vyvíjajúcich sa varietách. V neposlednom rade študujeme aplikácie v oblasti dynamiky fázových rozhraní a dislokačných slučiek v materiálovom výskume.
Výskum je zameraný na štúdium vlastností riešení nelineárnych difúznych rovníc a systémov, ako aj úloh s nelineárnymi a dynamickými okrajovými podmienkami. Okrem otázok spojených s existenciou a jednoznačnosťou sú vyšetrované najmä asymptotické vlastnosti riešení.

Výskumným cieľom je kvalitatívna a numerická analýza riešenia priamych a inverzných problémov s variačnou štruktúrou, ktoré môžu byť riešené pomocou moderných metód kónického programovania. Zameriavame sa na analýzu vlastností silnej duality pre dvojice primárnych a duálnych problémov pre triedy úloh kónického programovania. Identifikácia podmienok, ktoré už implikujú silnú dualitu aj pre nekonvexné problémy. Analyzujeme konvexné i nekonvexné priame a inverzné problémy prostredníctvom riešenia kónických optimalizačných úloh a ich relaxácií. Analyzujeme nelineárne problémy na vlastné hodnoty pre úlohy s variačnou štruktúrou a ich aplikácie v spektrálnej grafov. Metódy aplikujeme napríklad pre úlohu obálkovej analýzy dát pre triedu účelových funkcií s nelineárnou mierou efektívnosti obsahujúcich aj Russelovu hyperbolickú mieru efektívnosti, alebo na riešenie inverzného Wulffovho problému a konštrukcie optimálnej Finslerovej metriky.

Génová expresia predstavuje súbor procesov, ktorým sa informácia zakódovaná v genetickej predlohe používa na tvorbu aktívnych molekúl, predovšetkým bielkovín. Rozvoj nových technológií umožňujúcich meranie expresie génov na úrovní jednotlivých molekúl, jednotlivých buniek a v reálnom čase motivuje výskum matematických modelov popisujúcich dynamiku génovej expresie. Na katedre sa venujeme prístupom využívajúcim predovšetkým metodiku diferenciálnych rovníc a stochastických simulácií.
Cieľom výskumu je odhadnúť verejnozdravotný vplyv zmeny indikátorov očkovania na epidemiologickú situáciu. Vo výskume sa zameriavame na vysoko nákazlivé ochorenia a ich epidemické hrozby v krajinách EÚ. Pozornosť venujeme najmä dvom hlavným indikátorom očkovania: miere zaočkovanosti a včasnosti očkovania. Pomocou matematických a štatistických modelov predstavujeme viaceré možné očkovacie scenáre, ktorých verejno-zdravotný, sociálny a ekonomický dopad následne vyhodnotíme pomocou štatistických metód, prognózujeme epidemiologickú situáciu pri použití deterministických a stochastických modelov a vyhodnocujeme sociálny vplyv na jednotlivca a spoločnosť prostredníctvom QALY a DALY indikátorov.
Matematické modely v evolučnej genetike, v biofyzike buniek a vo fyziológii živočíchov pomáhajú porozumeniu princípom evolúcie a funkčnosti biologických druhov na makroskopickej aj mikroskopickej škále. V našom výskume sa venujeme štúdiu telomerickej DNA, ktorá sa podieľa na regulácii starnutia buniek, regulácii populačného rastu v kvasinkách, regulácii biorytmov pod vplyvom externého prostredia, či šíreniu výhodného génu v populácii. Okrem odpovedí na dôležité biologické otázky náš výskum otvára aj množstvo zaujímavých problémov na hrane súčasného matematického poznania, ktoré osobitne rigorózne študujeme.
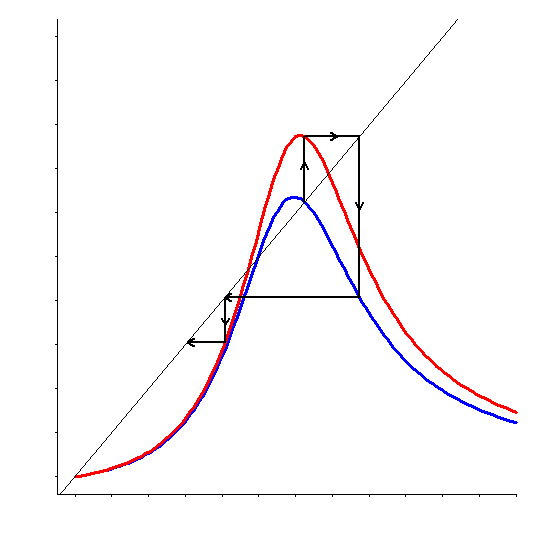
Náš výskum je zameraný na náhodné dynamické systémy generované spojitými zobrazeniami intervalu do seba a ich aplikácie, napríklad v populačnej dynamike. Zaoberáme sa najmä otázkami zložitosti takýchto systémov. Za istých podmienok sa môže systém ustáliť v nejakom ekvilibriu, teda jeho správanie je v istom zmysle jednoduché. Naopak, niekedy sa systém neustáli a jeho správanie sa dá považovať za chaotické. Na popísanie tejto zložitosti využívame niektoré pojmy súvisiace s chaosom známe z teórie diskrétnych dynamických systémov.

Vo výskume za zameriavame na kvalitatívnu a numerickú analýzu parciálnych diferenciálnych rovníc opisujúcich časový vývoj cien rôznych derivátov podkladových aktív, akými sú napríklad deriváty úrokovej miery alebo akcií. Zvláštnu pozornosť venujeme asymptotickej a perturbačnej analýze riešení v závislosti od parametrov a kalibrácií modelov na reálne trhové finančné dáta. Skúmame aj problémy vedúce na riešenie úloh o lineárnej komplementarite a variačným nerovnostiam, ktoré vznikajú pri oceňovaní amerických typov derivátov s predčasnou možnosťou uplatnenia a príslušným úlohám s voľnou hranicou.
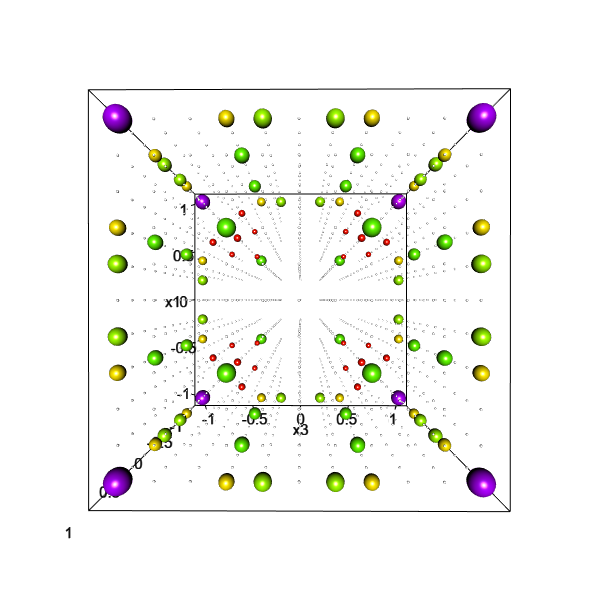
D-optimálny aproximatívny návrh experimentu pre kubický regresný model na kocke
Optimálny návrh experimentov je disciplína matematickej štatistiky, ktorá sa zaoberá metódami plánovania experimentu, s cieľom získať čo najväčšie množstvo informácie v rámci zadaných obmedzení na použiteľné zdroje, prípadne s cieľom zabezpečiť požadovanú kvalitu dát s čo najmenšími nákladmi. Výsledky výskumu v tejto disciplíne sú aplikovateľné v empirických vedách, v medicíne, priemysle, poľnohospodárstve, ale napríklad aj v prieskumoch obyvateľstva. Zakladateľom školy optimálneho navrhovania experimentov na KAMŠ je prof. RNDr. Andrej Pázman, DrSc., ktorý je súčasne jednou z vedúcich osobností tejto oblasti výskumu z celosvetového hľadiska.

Vo výskume sa zameriavame na analýzu špeciálnych tried rozdelení pravdepodobnosti. Navrhujeme a teoreticky charakterizujeme nové štatistické metódy pre rozdelenia pravdepodobnosti z týchto tried, ktoré sú zamerané hlavne na odhadovanie parametrov, posudzovanie vhodnosti modelov a parametrické i neparametrické štatistické testovanie. Tento štatistický aparát potom aplikujeme na špecifické problémy v metrológii, poistnej a finančnej matematike, lingvistike, demografii a v iných oblastiach. V rámci výskumného procesu pracujeme aj na počítačovej implementácii algoritmov a programových kódov pre spomínané štatistické postupy.
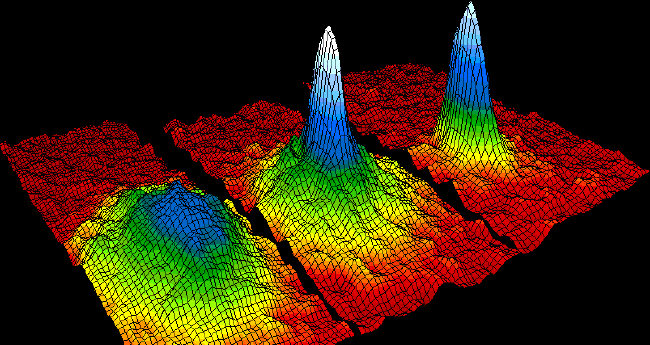
Stabilita riešení nelineárnych diferenciálnych rovníc hrá dôležitú rolu v mnohých aplikáciách v geofyzike, astrofyzike, materiálovom inžinierstve, mechanike tečenia tekutín, fyzike kondenzovaného stavu, evolučnej biológii, či v mnohých iných oblastiach. Okrem identifikovania stabilných stavov sú dôležitými otázkami zmeny stability pod vplyvom zmeny parametrov systému. V lineárnom priblížení je stabilita charakterizovaná spektrom príslušného operátora. Náš výskum sa zameriava na štúdium kvalitatívnych zmien spektra najmä prostredníctvom Kreinovej signatúry, ktorá identifikuje potenciálne nestabilné módy v Hamiltonovských systémoch.

Vo výskumnom tíme sa zameriavame predovšetkým na kvantitatívnu analýzu vlastností dôchodkových systémov a penzijných schém. V prípade akumulačnej fázy sporivých systémov porovnávame rôzne dynamické techniky riadenia portfólia a hľadáme optimálne investičné stratégie, ktoré maximalizujú budúci úžitok sporiteľov. Pri dekumulačnej fáze dôchodkových schém zas skúmame vplyv rizikových faktorov na výšku budúcich starobných dôchodkových dávok a venujeme sa aj analýze iných možných foriem vyplácania nasporených prostriedkov. Našim cieľom je, aby sme posunuli vpred výskum matematického modelovania fondovaných penzijných schém, vyvíjali dynamické regulačné stratégie na správu úspor a publikovali aplikovateľné výsledky najmä pre systém starobného dôchodkového sporenia na Slovensku.